Відсотки і все про них. Як скласти пропорцію? Зрозуміє будь-який школяр і дорослий

1. Що таке відсоток від числа
2. Обчислення відсотків за формулами
3. Розрахунки за допомогою пропорції
4. Альтернативний метод обчислень

Скласти пропорцію. У цій статті хочу поговорити з вами про пропорції. Розуміти, що таке пропорція, вміти складати її - це дуже важливо, вона дійсно рятує. Це начебто маленька і незначна «буква» у великій алфавіті математики, але без неї математика приречена бути кульгавий і неповноцінною.

Для початку нагадаю, що таке пропорція. Це рівність виду:

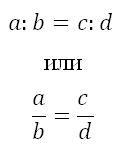
що те ж саме (це різна форма запису).

приклад:

Кажуть - один відноситься до двох також, як чотири відноситься до восьми. Тобто це рівність двох відносин (в даному прикладі відносини числові).

Основне правило пропорції:

a: b = c: d

твір крайніх членів дорівнює добутку середніх

тобто

a ∙ d = b ∙ c

Якщо яка-небудь величина в пропорції невідома, її можна знайти саме за цим правилом.

Якщо розглядати форму записи виду:

то використовують ще наступне правило, його називають «правило хреста»: записується рівність творів елементів (чисел або виразів) стоять по діагоналі

a ∙ d = b ∙ c

як бачите результат той же.

Якщо три елементи пропорції відомі, то

ми завжди можемо знайти четвертий.

Саме в цьому суть користі і необхідність

пропорції при вирішенні завдань.

Давайте розглянемо всі варіанти, де невідома величина х знаходиться в «будь-якому місці» пропорції, де a, b, c - числа:

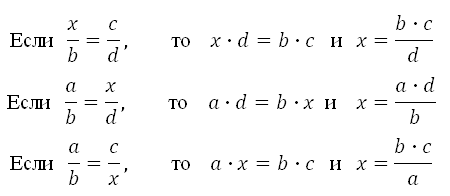
Величина стоїть по діагоналі від х записується в знаменник дробу, а відомі величини стоять по діагоналі записуються в чисельник, як твір. Його запам'ятовувати не обов'язково, ви і так все вірно обчисліть, якщо засвоїли основне правило пропорції.

тепер головне питання , Пов'язаний з назвою статті. Коли пропорція рятує і де використовується? наприклад:

1. Перш за все це завдання на відсотки. Ми розглядали їх в статтях "" і "".

2. Багато формули задані у вигляді пропорцій:

> Теорема синусів

> Відношення елементів у трикутнику

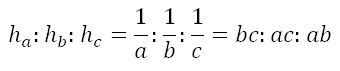
> Теорема тангенсов

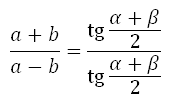
> Теорема Фалеса та інші.

3. У завданнях по геометрії в умови часто задається відношення сторін (інших елементів) або площ, наприклад 1: 2, 2: 3 і інші.

4. Переклад одиниць вимірювання, причому пропорція використовується для перекладу одиниць як в жодній мірі, так і для перекладу з однієї міри в іншу:

- годинник в хвилини (і навпаки).

- одиниці об'єму, площі.

- довжини, наприклад милі в кілометри (і навпаки).

- градуси в радіани (і навпаки).

тут без складання пропорції не обійтися.

Ключовий момент у тому, що потрібно правильно встановити відповідність, розглянемо прості приклади:

Необхідно визначити число, яке складає 35% від 700.

У завданнях на відсотки за 100% приймається та величина, з якої порівнюємо. Невідоме число позначимо як х. Встановимо відповідність:

Можна сказати, що семисот тридцяти п'яти відповідає 100 відсотків.

Іксу відповідає 35 відсотків. значить,

700 - 100%

х - 35%

вирішуємо

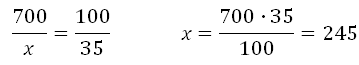
Відповідь: 245

Переведемо 50 хвилин в години.

Ми знаємо, що одній годині відповідає 60 хвилин.

x годин це 50 хвилин. значить,

1 - 60

х - 50

вирішуємо:

Тобто 50 хвилин це п'ять шостих години.

Відповідь: 5/6

Микола Петрович проїхав 3 кілометри. Скільки це буде в милях (врахувати, що 1 миля це 1,6 км)?

Відомо, що 1 миля це 1,6 кілометра. Число миль, які проїхав Микола Петрович приймемо за х. Чи можемо встановити відповідність:

Однією милі відповідає 1,6 кілометра.

Ікс миль це три кілометри.

1 - 1,6

х - 3

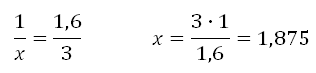
Відповідь: 1,875 миль

Ви знаєте, що для перекладу градусів у радіани (і назад) існують формули. Я їх не записую, так як запам'ятовувати їх вважаю зайвим, і так вам в пам'яті доводиться тримати багато інформації. Ви завжди зможете перевести градуси в радіани (і назад), якщо скористаєтеся пропорцією.

Переведемо 65 градусів в радіани міру.

Головне це запам'ятати, що 180 градусів це Пі радіан.

Позначимо шукану величину як х. Встановлюємо відповідність.

Ста вісімдесяти градусам відповідає Пі радіан.

Шістдесяти п'яти градусам відповідає х радіан. вивчити статтю по цій темі на блозі. Матеріал в ній викладено дещо по-іншому, але принцип той же. На цьому закінчу. Обов'язково буде ще що-небудь цікаве, не пропустіть!

Якщо згадати саме визначення математики, то в ньому є такі слова: математика вивчає кількісні ВІДНОСИНИ (ВІДНОСИНИ - тут ключове слово ). Як бачите в самому визначенні математики закладена пропорція. Вообщем, математика без пропорції це не математика !!!

Всього найкращого!

З повагою, Олександр Крутицький.

PS: Буду вдячний Вам, якщо розповісте про сайт в соціальних мережах.

Обчислення відсотків - нескладна математична операція, яка досить часто зустрічається в повсякденному житті . Наприклад, потрібно порахувати, скільки людина заощаджує, використовуючи дисконтну карту магазина або купуючи товар на розпродажі зі знижкою, під який відсоток бере кредит. Відсотки можна порахувати за допомогою калькулятора або пропорції, стане в нагоді формула обчислення відсотків і знання елементарних відомих співвідношень.

Що таке відсоток від числа

Обчислення відсотків в шкільній програмі вивчається класі в 5-м, якщо не раніше. Згідно з визначенням, відсоток - це одна сота частина числа. Термін з'явився в Стародавньому Римі і буквально перекладається як «зі ста». Спочатку ідея обчислювати відсотки зародилася ще в Вавилоні. Паралельно в Стародавній Індії навчилися рахувати відсотки за допомогою пропорції.

Для того щоб знайти відсоток від числа, необхідно дане число поділити на 100. Очевидно, що 1% від 100 дорівнює одиниці.

Обчислення відсотків за формулами

Формула, що дозволяє знайти відсоток від числа, елементарна. Необхідно число поділити на 100, після чого помножити на потрібний відсоток.

Якщо прийняти за Х вихідне число , А за Y - шуканий відсоток, то формула записується у вигляді X / 100 * Y = ...

Розрахунки за допомогою пропорції

Обчислення відсотків можна виробляти, маючи розуміння методу пропорції. Нехай А - основне число, прийняте за 100%, В - число, співвідношення якого з А в процентному співвідношенні необхідно вирахувати, а Х - число шуканих відсотків. тоді:

А - 100%,
В - Х%.

Множення хрест-навхрест дасть рівність: А * Х = В * 100. Отже, Х = В * 100 / А.

Наприклад, необхідно дізнатися, скільки відсотків від 300 становить число 75. Виходить: 75 * 100/300 = 25%.

Альтернативний метод обчислень

Уявімо один відсоток не десяткової, а простий дробом - 1/100. Аналогічно можна записати будь-яку кількість відсотків. Так, 10% - це 0,1 або 1/10, 25% - 0,25 або 25/100 = 1/4 і так далі. Отже, знайти 10% від числа досить просто - потрібно розділити вихідне число на 10. Таким способом зручно обчислювати 20, 25 і 50 відсотків:

• 20% - це 1/5, значить, потрібно ділити на 5 вихідне число.
• 25% - 1/4, потрібно ділити на 4.
• 50% - це 1/2, просто ділити на два.

Але не всякий відсоток зручно розрахувати таким методом. Наприклад, 33% - це 33/100, що під час запису десятковим дробом дає 0,3333 з безліччю трійок після коми.

Якщо виникають сумніви в правильності проведених розрахунків, завжди можна перевірити себе на калькуляторі, який зараз є в будь-якому мобільному пристрої і на будь-якому комп'ютері.

Це відношення, взяте в зворотному порядку по відношенню до даного. Ставлення b / a називають зворотним відношенню a / b. Пропорція - це рівність двох відносин. У пропорції (або a: b = з: d) числа a і d називають крайніми, а числа b і з - середніми членами пропорції. Основна властивість пропорції. У вірній пропорції твір крайніх членів дорівнює добутку її середніх членів. Якщо для двох відносин a: b і з: d виконується рівність ad = bс, то a: b = з: d - вірна пропорція. Якщо у вірній пропорції поміняти місцями середні члени або крайні члени, то отримані нові пропорції вірні. Перестановка членів пропорції: Похідні пропорції. Дана пропорція, справедливі наступні пропорції: Знаходження частини від числа Приклад 1. Знайти частина 5/16 від числа 800. Рішення. Якщо ви забули, яку дію треба зробити, існує такий прийом. Розберемося з «половиною», тобто 1/2 числа, на прикладі, який складемо самі. Наприклад, 1/2 від 800 ми розуміємо, що це 400. 800? 1/2 = 400. Який вплив ми зробили? Неважко здогадатися, що це множення. Тоді легко знайдемо 5/16 від 800 як 800 · 5/16 = 250. Відповідь: 250. Знаходження числа за його частини Приклад 2. Знайти всі число, якщо його 7/15 рівні 210. Рішення. З'ясуємо за допомогою «половини», тобто 1/2 числа, яке дію ми повинні зробити. Нехай, наприклад, треба знайти число, якщо його половина дорівнює 300. Очевидно, що це число 600. Яке дію ми зробили? 300? 1/2 = 600. Можна здогадатися, що цей розподіл. Тоді легко знайдемо чому дорівнює все число, якщо його 7/15 рівні 210: 210: 7/15 = 210 · 15: 7 = 450. Відповідь: 450. Приклад 3. Ставлення з до d одно 7/9. Знайдіть їх зворотне відношення. 1) - 7/9; 2); 3) 0,8; 4) 1,4. Рішення . Ставленням, зворотним до 7/9, є. Із запропонованих відповідей вірним є 2). Відповідь: 2. Приклад 4. Маса печива 15 кг, а маса упаковки 600 г. Знайдіть відношення маси печива до маси упаковки. 1) 15/600; 2) 5/6; 3) 1/25; 4) 25. Рішення . 600 г = 0,6 кг. Відношення маси печива до маси упаковки дорівнює 15 / 0,6 = 150/6 = 25. Із запропонованих відповідей вірним є 4). Відповідь: 4. Приклад 5. З яких відносин А = 4,8: ​​0,9; Б = 1,6: 0,3; В = 0,48: 0,9; Г = 25: 12 можна скласти пропорцію? 1) А і Б; 2) Б і В; 3) А і В; 4) Б і Г. Рішення . Перевіримо запропоновані відносини на виконання основного властивості пропорції. 1) Для відносин А і Б твір крайніх членів 4,8 · 0,3 = 1,44; твір середніх членів 0,9 · 1,6 = 1,44; 1,44 = 1,44. Отже, з цих відносин можна скласти пропорцію. 2) Для відносин Б і В твір крайніх членів 1,6 · 0,9 = 1,44; твір середніх членів 0,3 · 0,48 = 0,144; 1,44 0,144 3) Для відносин А і В твір крайніх членів 4,8 · 0,9 = 4,32; твір середніх членів 0,9 · 0,48 = 0,432; 4,32 0,432. Отже, з цих відносин не можна скласти пропорцію. 4) Для відносин Б і Г твір крайніх членів 1,6 · 12 = 19,2, твір середніх членів 0,3 · 25 = 7,5; 19,2 7,5. Отже, з цих відносин не можна скласти пропорцію. Із запропонованих відповідей вірним є 1). Відповідь: 1. Приклад 6. З пропорції 20: 15 = 16: 12 складено 4 рівності, вкажіть вірне. 1) 15: 20 = 16: 12; 2) 20: 12 = 15: 16; 3) 12: 16 = 15: 20; 4) 20: 16 = 12: 15. Рішення . Задана пропорція залишиться вірною, якщо в ній поміняти місцями середні або крайні члени. Отже, із запропонованих пропорцій вірною є тільки 3). Відповідь: 3. Приклад 7. Яке з перерахованих нижче рівності відносин складено невірно, якщо 13 · 6 = 0,78 · 100? 1) 13: 6 = 0,78: 100; 2) 13: 100 = 0,78: 6; 3) 6: 100 = 0,78 1 3; 4) 13: 0,78 = 100: 6. Рішення . З заданого рівності творів, на основі перестановки співмножників і основного властивості пропорції, можна скласти чотири вірні пропорції: 13: 0,78 = 100: 6; 6: 0,78 = 100: 13; 13: 100 = 0,78: 6; 6: 100 = 0,78: 13. Отже, із запропонованих відповідей невірним рівністю є 1). Відповідь: 1. Приклад 8. На пошиття 9 сорочок пішло 18,9 м тканини. Скільки метрів такої ж тканини потрібно на пошиття 15 сорочок? 1) 27; 2) 35; 3) 31,5; 4) 30. Рішення. Нехай на пошиття 15 сорочок потрібно х м тканини. Тоді, згідно з умовою, 9 сорочок - 18,9 м; 15 сорочок - х м Так як витрата тканини прямо пропорційний кількості сорочок, то справедлива рівність. За правилом знаходження крайнього члена пропорції х = 15 · 18,9: 9 = 31,5. Із запропонованих відповідей вірним є 3). Відповідь: 3. Приклад 9. За допомогою 6 однакових труб басейн заповнюється водою за 32 хвилини. За скільки хвилин можна заповнити басейн за допомогою 8 таких труб? 1) 36; 2) 42; 3) 64; 4) 24. Рішення. Нехай за допомогою 8 труб басейн можна заповнити за х хвилин. Тоді 6 труб - 32 хв; 8 труб - х хв. Так як час заповнення басейну обернено пропорційно кількості труб, то справедливо рівність 6: 8 = х: 32. За правилом знаходження середнього члена пропорції х = 6 · 32: 8 = 24. Із запропонованих відповідей вірним є 4). Відповідь: 4. Приклад 10. Кут в 140 ° розділений на 4 частини, градусні міри яких відносяться як 2: 3: 4: 5. Знайдіть градусну міру меншого з отриманих кутів. 1) 10 °; 2) 20 °; 3) 70 °; 4) 120 °. Рішення . Нехай х - градусна міра однієї частини. Тоді градусні міри кутів відповідно рівні 2х, Зх, 4х і 5х. Отже, 2х + Зх + 4х + 5х = 140; 14х = 140; х = 10; 10 ° - доводиться на одну частину. Градусна міра меншого з отриманих кутів дорівнює 2 · 10 ° = 20 °. Із запропонованих відповідей вірним є 2). Відповідь: 2. Приклад 11. Для будівництва стадіону 5 бульдозерів розчистили майданчик за 2 години 20 хвилин. За якийсь час 7 таких бульдозерів розчистять цей майданчик? 1) 7/5 ч; 2) 3 год 60 хв; 3) 1ч 40 хв; 4) 3 ч 16 хв. Рішення . Складемо пропорцію, враховуючи, що у нас зворотна пропорційність, тому що чим більше бульдозерів задіяно, тим менше час. 5 бульдозерів - 7/3 години 7 бульдозерів - х годин. 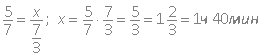, Що відповідає третьому варіанту. Відповідь: 3. Приклад 12. Качан капусти на 4/5 кг важче 4/5 цього ж качана. Яка маса капустини (в кг)? 1) 5; 2) 4,5; 3) 3; 4) 4. Рішення. Нехай качан капусти важить х кг. Тоді за умовою задачі 4 / 5х + 4/5 = х. Звідки знаходимо 1 / 5х = 4/5; х = 4 кг, що відповідає четвертому варіанту. Відповідь: 4. Приклад 13. Три числа відносяться як 8/19: 0,6: 93/95. Третє число більше половини першого на 36,5. Знайти більше з чисел. Рішення . Нехай перше число 8Х / 19; друге - 0,6Х; третє - 93х / 95. За умовою 3-е більше 1/2 першого на 36,5: 93/95 Х- 1/2 · 8/19 Х = 36,5; Х (93 / 95-4 / 19) = 73/2; 73/95 Х = 73/2; Х = 46,5. Тоді перше число (8/19) · 46,5 = 20; друге число 0,6 · 46,5 = 28,5; третє число (93/95) · 46,5 = 41,5 - найбільше з чисел. Відповідь: 41,5. Відсотки 1% - це сота (1/100) частина від цілого. Щоб знайти відсоток від числа, потрібно число відсотків представити у вигляді десяткового дробу і дане число помножити на цю десяткову дріб. Знайти відсоток від числа зводиться до задачі знаходження частини від числа. Знайти число за його відсотком зводиться до задачі знаходження числа за його частини. Формула простого процентного зростання (формула простих відсотків ): 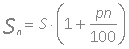, Де S n - нарощена сума ( початкова сума разом з нарахованими відсотками); S - початкова сума; р% - процентна ставка від суми, виражена в частках за період; n - число періодів нарахування. Знаходження відсотка від числа Відсоток - це сота частина числа. Значить, завдання зводиться до знаходження частини числа. Наприклад, 3% = 0,03; 0,15% = 0,015; 29,34% = 0,2934.

А) 6% від 20 - це 0,06 від 20, тобто 0,06 · 20 = 1,2. Б) 6% від Х - це 0,06Х.

Приклад 14. За планом добовий видобуток вугілля повинна бути 2860 тонн. Фактично шахта виконала 115% плану. Скільки це становить тонн? Рішення . 2860 · 115: 100 = 3289 (т) Відповідь: 3289. Знаходження числа за його відсотком Приклад 15. 15% становлять 30. Чому дорівнює все число? Рішення . Завдання зводиться до знаходження числа за його частини: 30: 0,15 = 30 · 100: 15 = 200. 2-й спосіб (пропорція):.

а) Х + 0,03Х = 1,03Х; б) Х + 0,17Х = 1,17Х; в) Х + 0,32Х = 1,32Х.

Приклад 18. Число Х зменшити на а) 3%, б) 17%, в) 32%. Рішення .

а) Х - 0,03Х = 0,97Х; б) Х - 0,17Х = 0,83Х; в) Х - 0,32Х = 0,68Х.

Приклад 19. А дорожче В на 25%. На скільки відсотків В дешевше А? Рішення . Ті, хто вирішив, що відповідь 25% - помилилися. А більше В на 25%, тобто А = 1,25В. Звідси В = А: 1,25 = 0,8 А. Запис В = 0,8 А означає, що В дешевше А на 20%. Відповідь: 20%. Приклад 20. Метод швидкісного випалу цегли дозволяє збільшити випуск цегли з 1200 до 2300 штук. На скільки відсотків при цьому збільшилося виробництво цегли (відповідь округлити до цілих)? Рішення .

1-й спосіб 2300 1200 · 100 = 192%; 192 - 100 = 92%. 2-й спосіб 2300 - 1200 = 1100; 1100 1200 · 100 = 92%.

Відповідь: 92. Приклад 21. Скільки коштував метр тканини до зниження цін, якщо після зниження продажної ціни на 15%, ця тканина продається по 1200 рублів за метр. Невірне рішення:

1) 15% від 1200 це 1200 · 0,15 = 180 (грн.) 2) 1200 + 180 = 1280 (руб.) - коштував метр тканини до зниження цін.

Це НЕВІРНО, тому що відсоток зниження встановлюється по відношенню до колишніх цін. ПРАВИЛЬНЕ рішення: Після зниження цін вартість тканини склала 100 - 15 = 85% від колишньої ціни. Тому колишня ціна становила (див. Приклад 15) 1200: 0,85 = 1411 руб. 76 коп. або 1411,76 руб. Відповідь: 1411,76. Відеолекція «Відносини. Пропорції. Відсотки »: